突然ですが問題です！
　以下のような３ｍ×３ｍの正方形の内部（周上を含む）に１０個の石を投げ入れます。そのとき、間の距離が１．５ｍ未満である２つの石が必ず存在することを示しなさい。

 

 

 

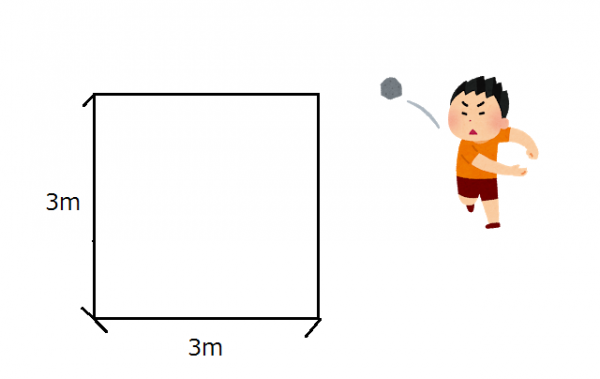
　この問題を見て少し考えた後、多くの人はこう思うのではないでしょうか？

「よぉわからんけど、たぶんそうなるやろ」

　そうなんです！なるんです！実際に図なんか書いてみると必ずそうなります。
　しかし、この問題は“示しなさい”。つまり理由を付けて説明しないといけないのです。さあどうしましょう・・・。

 

 

　一人で考えても思いつかない時は誰かに手伝ってもらいましょう。そうですねぇ・・・じゃあ今回は鳩に手伝ってもらいましょう！！

 

　以下のような巣箱に７羽の鳩を入れるとします。

 

 

 

 

 

６羽目までは１羽につき１つの巣箱がありますよね？しかし７羽目が入ろうと思っても既にすべての巣に鳩が入っていますので、相席になってしまいます。

　このように「ｎ個の箱に（ｎ+１）個以上のものをいれるとき、必ず２つ以上のものが入る箱が１つ以上存在する」ことを「鳩ノ巣原理」といいます。

　この「鳩ノ巣原理」なのですが、中学・高校の教科書には登場しないのですが、知っていれば楽に解けるような問題が入試などで出題されることが、たまにあります。

 

　さて、それでは初めの問題に戻ってみましょう。

 

 

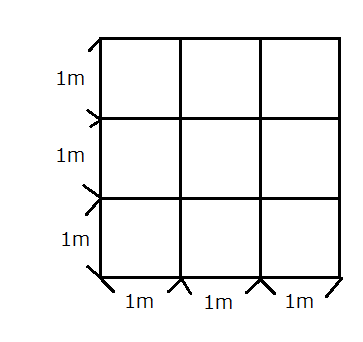
　一辺１ｍの正方形が９つできるように、縦横に線を引いてみます。そうすると９つの「箱」が出来ました。ここに１０個の石（＝鳩）を入れようとすると、鳩ノ巣原理より２つ以上の石が入ってしまう正方形（＝箱）が１つ以上存在します。

 

 

 

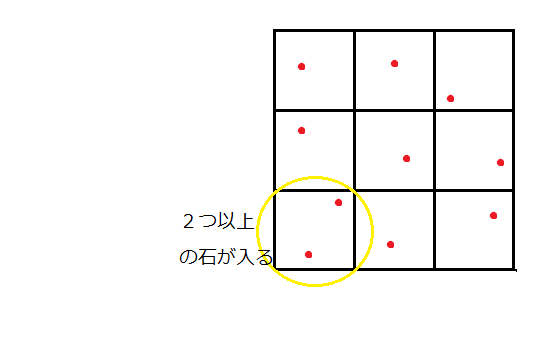
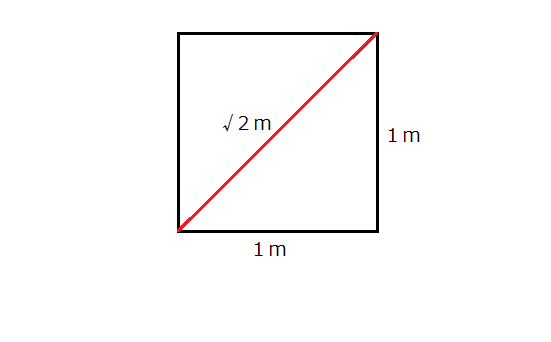
　その正方形の中で２つの石が最も離れている場合、一辺１ｍの正方形の対角線に当たりますので、三平方の定理（わからない人は調べてね）より、その距離は√2ｍ！
　つまり1.41421356…..ｍ（ヒトヨヒトヨニヒトミゴロと覚えましたよね）ですので、最大でも約1.4ｍしか離れることができないということになるので、もちろん1.5ｍ未満であるということもできます！

 

 

 

感覚ではわかることでも、きっちり説明するのは難しい。そんなときは鳩のことを思い出してみてください。

塾長　いしき